We will cover following topics

Assignment Problems

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of the Assignment Problem

Suppose there are $n$ jobs to be performed and $n$ persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let $c_{ij}$ be the cost if the $i-th$ person is assigned to the $j-th$ job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

Mathematical Formulation of the Assignment Problem

An assignment problem can be mathematically formulated as follows:

Minimise the total cost

\[Z= \sum_{i=1}^n\sum_{j=1}^n c_{ij}.x_{ij}\]

where

$x_{ij} =1$, if $i^{th}$ person is assigned to the $j^{th}$ job
$x_{ij}=0$, if $i^{th}$ person is that assigned to the $j^{th}$ job

subject to the constraints

i) $\sum_{i=1}^n x_{ij} = 1, j=1, 2, \cdots n$

which means that only one job is done by the $i^{th}$ person, $i= 1, 2, \cdots, n$

ii) $\sum_{i=1}^n x_{ij} = 1, j=1, 2, \cdots n$

which means that only one person should be assigned to the $j^{th}$ person, $j= 1, 2, \cdots, n$

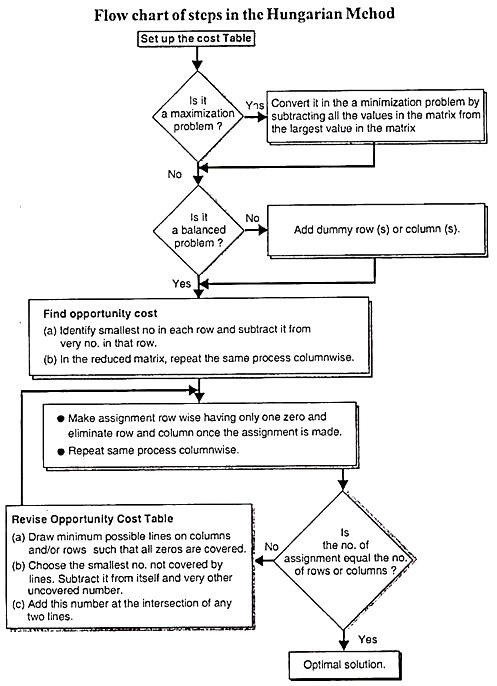
Hungarian Method for Solving Assignment Problem

The Hungarian method of assignment provides us with an efficient method of finding the optimal solution without having to make a-direct comparison of every solution. It works on the principle of reducing the given cost matrix to a matrix of opportunity costs.

Opportunity cost show the relative penalties associated with assigning resources to an activity as opposed to making the best or least cost assignment. If we can reduce the cost matrix to the extent of having at least one zero in each row and column, it will be possible to make optimal assignment.

The Hungarian method can be summarized in the following steps:

Step 1: Develop the Cost Table from the given Problem

If the no of rows are not equal to the no of columns and vice versa, a dummy row or dummy column must be added. The assignment cost for dummy cells are always zero.

Step 2: Find the Opportunity Cost Table

(a) Locate the smallest element in each row of the given cost table and then subtract that from each element of that row, and

(b) In the reduced matrix obtained from 2 (a) locate the smallest element in each column and then subtract that from each element. Each row and column now have at least one zero value.

Step 3: Make Assignment in the Opportunity Cost Matrix

The procedure of making assignment is as follows:

(a) Examine rows successively until a row with exactly one unmarked zero is obtained. Make an assignment single zero by making a square around it.

(b) For each zero value that becomes assigned, eliminate (Strike off) all other zeros in the same row and/ or column

(d) If a row and/or column has two or more unmarked zeros and one cannot be chosen by inspection, then choose the assigned zero cell arbitrarily.

(e) Continue this process until all zeros in row column are either enclosed (Assigned) or struck off (x)

Step 4: Optimality Criterion

If the member of assigned cells is equal to the numbers of rows column then it is optimal solution. The total cost associated with this solution is obtained by adding original cost figures in the occupied cells.

If a zero cell was chosen arbitrarily in step (3), there exists an alternative optimal solution. But if no optimal solution is found, then go to step (5).

Step 5: Revise the Opportunity Cost Table

Draw a set of horizontal and vertical lines to cover all the zeros in the revised cost table obtained from step (3), by using the following procedure:

(a) For each row in which no assignment was made, mark a tick (√)

(b) Examine the marked rows. If any zero occurs in those columns, tick the respective rows that contain those assigned zeros.

If a no of lines drawn is equal to the no of (or columns) the current solution is the optimal solution, otherwise go to step 6.

Step 6: Develop the New Revised Opportunity Cost Table

(a) From among the cells not covered by any line, choose the smallest element, call this value K

(b) Subtract K from every element in the cell not covered by line.

(d) Elements in cells covered by one line remain unchanged.

Step 7: Repeat Step 3 to 6 Unlit an Optimal Solution is Obtained

Flow Chart of Hungarian Method

The flow chart of steps in the Hungarian method for solving an assignment problem is shown in following figures:

Assignment Problems

PYQs

Assignment Problems

1) $$\begin{array}{

} \hline {} & {M_1} & {M_2} & {M_3} & {M_4} & {M_5} \ \hline {O_1} & {24} & {29} & {18} & {32} & {19} \ \hline {O_2} & {17} & {26} & {34} & {22} & {21} \ \hline {O_3} & {27} & {16} & {28} & {17} & {25} \ \hline {O_4} & {22} & {18} & {28} & {30} & {24} \ \hline {O_5} & {28} & {16} & {31} & {24} & {27} \ \hline \end{array}$$

In a factory there are five operator $O_1$, $O_2$, $O_3$, $O_4$, $O_5$ and five machine $M_1$, $M_2$, $M_3$, $M_4$, $M_5$. The operating costs are given when the $O_i$ operator operates the $M_j$ machine $(i,j=1,2,..,5)$. But there is a restriction that $O_3$ cannot be allowed to operate the third machine $M_3$ and $O_2$ cannot be allowed to operate the fifth machine $M_5$. The cost matrix is given above. Find the optional assignment and the optimal assignment cost also.

[2018, 15M]

2) Solve the following assignment problem to maximize the sales:
$\begin{array}{|c|c|c|c|c|c|} \hline {} & {I} & {II} & {III} & {IV} & {V} \\ \hline {A} & {3} & {4} & {5} & {6} & {7} \\ \hline {B} & {4} & {15} & {13} & {7} & {6} \\ \hline {C} & {6} & {13} & {12} & {5} & {11} \\ \hline {D} & {7} & {12} & {15} & {8} & {5} \\ \hline {E} & {8} & {13} & {10} & {6} & {9} \\ \hline \end{array}$

where $I$, $II$, $III$, $IV$ and $V$ are Territories;
$A$, $B$, $C$, $D$, $E$ are Salesmen.

[2015, 10M]

3) Solve the minimum time assignment problem:
$\begin{array}{|c|c|c|c|c|} \hline { } & {I} & {II} & {III} & {IV} \\ \hline {A} & {3} & {12} & {5} & {4} \\ \hline {B} & {7} & {9} & {8} & {12} \\ \hline {C} & {5} & {11} & {10} & {12} \\ \hline {D} & {6} & {14} & {4} & {11} \\ \hline \end{array}$

where $I$, $II$, $III$ and $IV$ are Machines;
$A$, $B$, $C$ and $D$ are Jobs.

[2013, 15M]

4) A travelling salesman has to visit 5 cities. He wishes to start from a particular city, visit each city once and then return to his starting point. Cost of going from one city to another is given below:

\[\begin{array}{|c|c|c|c|c|c|} \hline { } & {A} & {B} & {C} & {D} & {E} \\ \hline {A} & {\infty} & {4} & {10} & {14} & {2} \\ \hline {B} & {12} & {\infty} & {6} & {10} & {4} \\ \hline {C} & {16} & {14} & {\infty} & {8} & {14} \\ \hline {D} & {24} & {8} & {12} & {\infty} & {10} \\ \hline {E} & {2} & {6} & {4} & {16} & {\infty} \\ \hline \end{array}\]

You are required to find the least cost route.

[2004, 15M]

5) Find the optimal solution for the assignment problem with the following cost matrix:
$\begin{bmatrix}{6} & {1} & {9} & {11} & {12} \\ {2} & {8} & {17} & {2} & {5} \\ {11} & {8} & {3} & {3} & {3} \\ {4} & {10} & {8} & {6} & {11} \\ {8} & {10} & {11} & {5} & {13}\end{bmatrix}$

Indicate clearly the rule you apply to arrive at the complete assignment.

[2003, 15M]

< Previous Next >